HUBUNGAN ANTAR SUDUT (2) HUBUNGAN SUDUT-SUDUT PADA DUA GARIS SEJAJAR

Kompetensi Dasar :
3.10 Menganalisis hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal.


HUBUNGAN ANTAR SUDUT (2) HUBUNGAN SUDUT-SUDUT PADA DUA GARIS SEJAJAR

Pada bagian hubungan antar sudut (1), sudah dijelaskan hubungan antar sudut yang saling berpelurus, saling berpenyiku dan saling bertolak belakang. Untuk postingan ini akan dijelaskan materi hubungan antar sudut bagian 2 yang berisi tentang hubungan sudut-sudut pada dua garis sejajar. apa saja yang akan kita pelajari? langsung saja perhatikan penjelasan berikut ini.


HUBUNGAN SUDUT-SUDUT PADA DUA GARIS SEJAJAR
Perhatikan gambar berikut.

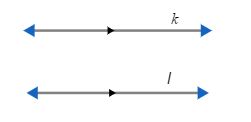gb1. garis k sejajar dengan garis l

Garis k dan garis l  di samping merupakan 2 garis yang saling sejajar.

bagaimana jadinya kalau terdapat garis lain yang memotong 2  garis yang sejajar tersebut?

Lihat gambar selanjutnya.

gb2. Garis m memotong garis k dan garis l membentuk  titik A dan B

Garis m (garis berwarna merah) memotong garis k dan garis l yang saling sejajar sehingga terbentuk 2 titik potong yaitu titik A dan titik B.

Ada berapa sudut yang terbentuk dari  pemotongan garis m terhadap garis k dan garis l?

gb3. terbentuknya 8 sudut dari garis m yang memotong garis k dan garis l

Gambar di samping menunjukkan banyak sudut yang terbentuk adalah 8 sudut. Sudut apa sajakah?
∠A₁, ∠A₂, ∠A₃, ∠A₄
∠B₁, ∠B₂, ∠B₃, ∠B₄

Ternyata jika terdapat sebuah garis memotong 2 garis yang saling sejajar mengakibatkan terbentuknya 8 sudut.

Adakah hubungan antara kedelapan sudut tersebut?

Simak penjelasan selanjutnya


Ada 5 hubungan sudut-sudut pada dua garis sejajar, yaitu sudut sehadap, sudut dalam berseberangan, sudut luar berseberangan, sudut dalam sepihak, dan sudut luar sepihak.

A. SUDUT SEHADAP
     Perhatikan gambar berikut!

Dari gambar di samping dapat di lihat ∠A₁ menghadap sesuai tanda panah merah, begitu pula ∠B₁ juga menghadap sesuai tnda panah merah.

Karena ∠A₁  dan ∠B₁ menghadap ke arah yang sama maka dapat dikatakan ∠A₁  dan ∠B₁ merupakan sudut sehadap dan memiliki ukuran sudut yang sama besar, sehingga m∠A₁  = m∠B₁

Begitu halnya dengan sudut ∠A₂ dan ∠B₂ sama-sama menghadap pada arah tanda panah merah.

Karena menghadap ke arah yang sama maka ∠A₂ dan ∠B₂  merupakan sudut sehadap memiliki ukuran sudut yang sama besar, sehingga m∠A₂ = m∠B₂

Selain ∠A₁  dan ∠B₁ serta ∠A₂ dan ∠B₂ yang Saling sehadap, sudut manalagi yang saling sehadap?

Sudut-sudut lain yang saling sehadap adalah
∠A₃ dan ∠B₃ ⇔ m∠A₃ = m∠B₃                        
∠A₄ dan ∠B₄ ⇔ m∠A₄ = m∠B₄


B. SUDUT DALAM BERSEBERANGAN 
     Perhatikan gambar berikut!

Dari gambar di samping terdapat dua daerah dimana daerah antara 2 garis sejajar (daerah berwarna biru) merupakan daerah dalam, sedangkan daerah diluar 2 garis sejajar (daerah warna kuning) merupakan daerah luar.

Berdasarkan daerahnya terdapat beberpa sudut yang terletak di daerah dalam dan beberapa sudut yang terletak di daerah luar.

Sudut apa sajakah yang terletak di daerah dalam?
Sudut yang terletak di daerah dalam yaitu ∠A₃, ∠A₄, ∠B₁, dan ∠B₂ .

    Selanjutnya sudut apa sajakah yang terletak di daerah luar?
    Sudut yang terletak di daerah luar yaitu ∠A₁, ∠A₂, ∠B₃, dan ∠B₄ .

    Sampai di ini jelas ya?

   Kita lanjutkan dengan sudut dalm berseberangan, apa itu?
   Perhatikan gambar berikut!
 

Lihat  ∠A₃ dan ∠B₁
Kedua sudut tersebut terletak di daerah dalam dan saling menyeberangi garis merah (garis m).

Karena kedua sudut tersebut terletak di daerah dalam dan berseberangan maka ∠A₃ dan ∠B₁ merupakan sudut dalam berseberangan  dan besar sudutnya sama.

Sehingga m∠A₃ = m∠B₁

Begitu juga dengan sudut ∠A₄ dan ∠B₂
Kedua sudut tersebut terletak di daerah dalam dan saling menyeberangi garis merah (garis m).

Karena kedua sudut tersebut terletak di daerah dalam dan berseberangan maka ∠A₄ dan ∠B₂ merupakan sudut dalam berseberangan  dan besar sudutnya sama.

Sehingga m∠A₄ = m ∠B₂

C. SUDUT LUAR BERSEBERANGAN 
     Perhatikan gambar berikut!

Sudut Luar Berseberangan tidak berbeda jauh dengan sudut dalam berseberangan, yang membedakan hanya letak sudut-sudut tersebut berada di daerah luar dan tetap saling menyeberang garis m (garis merah).

Oleh karena itu, sudut-sudut luar berseberangan yaitu
∠A₁ dan ∠B₃
∠A₂ dan ∠B₄

 Sudut-sudut luar berseberangan juga memiliki ukuran sudut yang sama besar.
 Sehingga,
 m∠A₁ = m∠B₃
 m∠A₂ = m∠B₄


D. SUDUT DALAM SEPIHAK
      Perhatikan gambar berikut!

Lihat  ∠A₄ dan ∠B₁
Kedua sudut tersebut terletak di daerah dalam dan terletak di sebelah kiri garis m (garis merah).

Karena kedua sudut tersebut terletak di daerah dalam dan sama-sama terletak di sebelah kiri garis m (garis merah) maka∠A₄ dan ∠B₁ merupakan sudut dalam sepihak. 

Sudut dalam sepihak ini berbeda dengan sudut sehadap, sudut dalam berseberangan, maupun sudut luar berseberangan.

Jika sudut sehadap, sudut dalam berseberangan, maupun sudut luar berseberangan memiliki ukuran yang sama besar, untuk sudut dalam sepihak ini jika kedua sudut di tambahkan besarnya 180⁰

Sehingga m∠A₄ + m∠B₁ = 180⁰

Begitu juga hubungan antara sudut  ∠A₃ dan ∠B₂.

Kedua sudut tersebut terletak di daerah dalam dan sama-sama terletak di sebelah kanan garis m (garis merah) maka ∠A₃ dan ∠B₂. merupakan sudut dalam sepihak. 

Sehingga m∠A₃ + m∠B₂ = 180⁰

E. SUDUT LUAR SEPIHAK
    Perhatikan gambar berikut!

Sudut luar sepihak tidak berbeda dengan sudut dalam sepihak, hanya yang membedakan adalah letak sudut berada di daerah luar dan sama-sama berada di pihak yang sama.

Dari gambar di atas sudut-sudut luar sepihak adalah
∠A₁ dan ∠B₄
∠A₂ dan ∠B₃

Karena ukuran sudut - sudut luar sepihak jika di jumlahkan hasilnnya 180⁰, maka berlaku
m∠A₁ + m∠B₄ = 180⁰
m∠A₂ + m∠B₃ = 180⁰



Kesimpulan:
Pada dua garis sejajar yang dipotong garis lain seperti gambar berikut

A. Sudut-sudut yang saling sehadap adalah :
    ∠A₁ dan ∠B₁, sehingga m∠A₁  = m∠B₁
    ∠A₂ dan ∠B₂, sehingga m∠A₂ = m∠B₂
    ∠A₃ dan ∠B₃, sehingga m∠A₃ = m∠B₃  
    ∠A₄ dan ∠B₄, sehingga m∠A₄ = m∠B₄

    Sudut yang saling berhadapan memiliki besar sudut        yang sama. 


B. Sudut-sudut dalam berseberangan adalah :
    ∠A₃ dan ∠B₁, sehingga m∠A₃ = m∠B₁
    ∠A₄ dan ∠B₂, sehingga m∠A₄ = m ∠B₂
 Sudut-sudut dalam berseberangan memiliki besar sudut yang sama. 

C. Sudut-sudut luar berseberangan adalah :
    ∠A₁ dan ∠B₃, sehingga m∠A₁ = m∠B₃
    ∠A₂ dan ∠B₄, sehingga m∠A₂ = m∠B₄
    Sudut-sudut luar berseberangan memiliki besar sudut yang sama. 

D. Sudut-sudut dalam sepihak adalah :
    ∠A₄ dan ∠B₁, sehingga m∠A₄ + m∠B₁ = 180⁰
    ∠A₃ dan ∠B₂, sehingga m∠A₃ + m∠B₂ = 180⁰
    Sudut-sudut dalam sepihak memiliki sifat jika ukuran kedua sudut di jumlahkan hasilnya          adalah 180⁰

E. Sudut-sudut luar sepihak adalah :
    ∠A₁ dan ∠B₄, sehingga m∠A₁ + m∠B₄ = 180⁰
    ∠A₂ dan ∠B₃, sehingga m∠A₂ + m∠B₃ = 180⁰
    Sudut-sudut luar sepihak memiliki sifat jika ukuran kedua sudut di jumlahkan hasilnya           adalah 180⁰


Contoh Soal 1
Perhatikan gambar berikut!

Tentukan nilai x!

Pembahasan
2x+10⁰ = 70⁰      (sudut sehadap sama besar)
⇔ 2x = 70⁰- 10⁰
⇔ 2x = 60⁰
⇔ x = 60⁰ : 2
⇔ x = 30⁰

Contoh Soal 2
Perhatikan gambar berikut!

Tentukan nilai x!

Pembahasan
3x+60⁰ = 120⁰ (sudut dalam berseberangan sama besar)
⇔ 3x = 120⁰- 60⁰
⇔ 3x = 60⁰
⇔ x = 60⁰ : 3
⇔ x = 20⁰

Contoh Soal 3
Perhatikan gambar berikut!

Tentukan nilai x!

Pembahasan
(8x+5⁰)+ 135⁰= 180⁰ (sudut luar sepihak jika dijumlahkan sama dengan 180⁰ )
(8x+5⁰)+ 135⁰= 180⁰
⇔ 8x + 140⁰ = 180⁰
⇔ 8x = 180⁰- 140⁰
⇔ 8x = 40⁰
⇔ x = 40⁰ : 8
⇔ x = 5⁰

Contoh Soal 4
Perhatikan gambar berikut!

Tentukan nilai a+b!











Pembahasan
i) menentukan nilai a
   3a⁰+ 105⁰= 180⁰ (sudut luar sepihak jika  dijumlahkan sama dengan 180⁰ )
     3a⁰+ 105⁰= 180⁰
    ⇔ 3a⁰= 180⁰ - 105⁰
    ⇔ 3a⁰= 75⁰
    ⇔  a= 75 : 3
    ⇔ a = 25

ii) menentukan nilai b
   3b⁰= 3a⁰ (sudut luar bersebarangan sama besar)
    ⇔3b⁰= 3. 25⁰
    ⇔ 3b⁰= 75⁰
    ⇔  b= 75 : 3
    ⇔ b = 25

iii) nilai a+b = 25 + 25 = 50



Materi hubungan sudut-sudut pada dua garis sejajar beserta contoh soal sudah saya jelaskan secara runtut.
bagaimana setelah kalian membaca materi di atas?

Apakah materi mudah dipahami?
Mohon jawab di kolom komentar ya!

Semoga materi ini bermanfaat Aamiin

Hubungan Antar Sudut (1)

Kompetensi Dasar :
3.10 Menganalisis hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal.

HUBUNGAN ANTAR SUDUT (1)

Hubungan antar sudut bagian 1 ini akan menjelaskan hubungan antar sudut yang saling berpelurus, berpenyiku, dan saling bertolak belakang. sedangkan hubungan antar sudut pada garis yang sejajar akan dijelaskan pada postingan selanjutnya yaitu hubungan antar sudut bagian (2).

Berikut saya sampaikan materi dan contoh soalnya, semoga materi dapat dipahami dengan mudah dan menjadikan kalian suka dengan matematika.

Sebelum membahas hubungan antar sudut ini, kita ingat kembali jenis-jenis sudut yang sudah kita pelajari.

JENIS-JENIS SUDUT

1. Sudut lancip, yaitu sudut yang ukuran sudutnya antara 0⁰ sampai 90⁰
2. Sudut siku-siku,  yaitu sudut yang ukuran sudutnya 90⁰
3. Sudut tumpul, yaitu sudut yang ukuran sudutnya antara 90⁰ sampai 180⁰
4. Sudut lurus,  yaitu sudut yang ukuran sudutnya 180⁰
5. Sudut reflek, yaitu sudut yang ukuran sudutnya antara 180⁰ sampai 360⁰

A. SUDUT BERPELURUS (BERSUPLEMEN)
Perhatikan gambar sudut berikut!

besar sudut AOB (m∠AOB) adalah 180⁰ (sudut lurus)

Dari titik O dibuat sinar garis OC sehingga gambar menjadi seperti di samping.
Terbentuk 2 sudut berbeda yaitu ∠AOC dan ∠BOC


Sehingga, jika ∠AOC dan ∠BOC digabung akan membentuk ∠AOB 

Jadi,
m∠AOC + m∠BOC =m∠AOB
m∠AOC + m∠BOC = 180⁰   

karena besar sudut ∠AOC ditambah besar sudut ∠BOC yaitu 180⁰, maka hubungan antara sudut AOC dan sudut BOC disebut sudut berpelurus (bersuplemen)

Istilah lain
∠AOC = pelurus ∠BOC
          atau
∠BOC = pelurus ∠AOC

Oleh karena itu,
Jika m∠BOC = α dan m∠AOC = β, 
maka 
m∠BOC + m∠AOC =180⁰
⇔  α + β = 180⁰
⇔  α = 180⁰ - β
         atau
⇔  α + β = 180⁰
⇔   β = 180⁰ - α

diperoleh
α = 180⁰ - β ⇔  m∠BOC =180⁰ - m∠AOC 
β = 180⁰ - α ⇔  m∠AOC =180⁰ - m∠BOC 

KESMIPULAN
Sudut Berpelurus (bersuplemen) adalah hubungan dua sudut yang mana jika kedua sudut tersebut digabungkan menjadi sudut lurus.

Contoh soal 1

Perhatikan gambar berikut!

Jika m∠BOC = 50⁰, besar sudut AOC adalah ....




Pembahasan
m∠AOC + m∠BOC =180⁰ (karena saling berpelurus)
⇔  m∠AOC + 50⁰ =180⁰
⇔  m∠AOC  =180⁰ -  50⁰
⇔  m∠AOC  =130⁰

atau
m∠AOC  =180⁰ - m∠BOC 
⇔  m∠AOC  =180⁰ -  50⁰
⇔  m∠AOC  =130⁰


Contoh soal 2

Perhatikan gambar berikut!

Tentukan
a. nilai x
b. besar sudut AOC


Pembahasan
a. menentukan nilai x
m∠AOC + m∠BOC =180⁰ (karena saling berpelurus)
⇔  4x⁰ +  2x⁰=180⁰
⇔  6x⁰ = 180⁰
⇔  x = 180 : 6
⇔  x = 30
jadi, nilai x adalah 30

b.  menentukan m∠AOC
m∠AOC =4x⁰   (nilai  x = 30 sudah di temukan pada pembahasan a.)
⇔ m∠AOC =4.(30)⁰
⇔ m∠AOC =120⁰
jadi, besar sudut AOC adalah 120⁰


contoh soal 3
Perhatikan gambar berikut!

Tentukan
a. besar sudut BOC
b. besar pelurus sudut BOC




a. menentukan nilai x terlebih dahulu
m∠AOC + m∠BOC =180⁰ (karena saling berpelurus)
⇔  (3x-5)⁰ +  (5x+25)⁰=180⁰
⇔  (3x+5x-5+25)⁰ = 180⁰
⇔  (8x+20)⁰ = 180⁰
⇔  8x = 180 - 20
⇔  8x = 160
⇔  x = 160 : 8
⇔  x = 20
jadi, nilai x adalah 20

kemudian menentukan m∠BOC
m∠BOC =(5x+25)⁰  (nilai  x = 20 sudah di temukan pada pembahasan a.)
⇔ m∠BOC =(5.(20)+25)⁰
⇔ m∠BOC =(100+25)⁰
⇔ m∠BOC =125⁰
jadi, besar sudut BOC adalah 125⁰

b. menentukan besar pelurus sudut BOC
pelurus ∠BOC = ∠AOC   (ingat ya ∠AOC  adalah pelurus dari ∠BOC)
maka, 
m∠AOC= 180⁰ - m∠BOC
⇔ m∠AOC= 180⁰ - 125⁰
⇔ m∠AOC= 55⁰
jadi, besar pelurus sudut BOC adalah 55⁰


B. SUDUT BERPENYIKU (BERKOMPLEMEN)
Perhatikan gambar sudut berikut!

besar sudut ABC (m∠ABC) adalah 90⁰ (sudut siku-siku)

Dari titik B dibuat sinar garis BD sehingga gambar menjadi seperti di samping.

Terbentuk 2 sudut berbeda yaitu ∠ABD dan ∠CBD.
Sehingga, jika ∠ABD dan ∠CBD digabung akan membentuk ∠ABC 

Jadi,
m∠ABD + m∠CBD = m∠ABC
m∠ABD + m∠CBD = 90⁰

karena besar sudut ∠ABD ditambah besar sudut m∠CBD yaitu 90⁰, maka hubungan antara sudut ABD dan sudut CBD disebut sudut berpenyiku  (berkomplemen)

Istilah lain
∠ABD  = penyiku ∠CBD
          atau
∠CBD = penyiku ∠ABD 

Oleh karena itu,
Jika m∠ABD  = α dan m∠CBD = β, 
maka 
m∠ABD + m∠CBD = 90⁰
⇔  α + β = 90⁰
⇔  α = 90⁰ - β
         atau
⇔  α + β = 90⁰
⇔   β = 90⁰ - α

diperoleh
α = 180⁰ - β ⇔  m∠ABD  = 90⁰ - m∠CBD 
β = 180⁰ - α ⇔  m∠CBD = 90⁰ - m∠ABD 

KESMIPULAN
Sudut Berpenyiku (berkomplemen) adalah hubungan dua sudut yang mana jika kedua sudut tersebut digabungkan menjadi sudut siku-siku.

Contoh soal 1

Perhatikan gambar berikut!

Jika m∠CBD = 35⁰, besar sudut ABD adalah ....

Pembahasan
m∠ABD + m∠CBD = 90⁰ (karena saling berpenyiku)
⇔  m∠ABD+ 35⁰ =90⁰
⇔  m∠ABD  =90⁰ -  35⁰
⇔  m∠ABD  =55⁰

atau
m∠ABD  =90⁰ - mm∠CBD 
⇔  m∠ABD  =90⁰ -  35⁰
⇔  m∠ABD  =55⁰


Contoh soal 2

Perhatikan gambar berikut!

Tentukan
a. nilai x
b. besar sudut CBD




Pembahasan
a. menentukan nilai x
m∠ABD + m∠CBD = 90⁰ (karena saling berpenyiku)
⇔  6x⁰ +  3x⁰=90⁰
⇔  9x⁰ = 90⁰
⇔  x = 90 : 9
⇔  x = 10
jadi, nilai x adalah 10

b.  menentukan m∠CBD
m∠CBD =3x⁰   (nilai  x = 10 sudah di temukan pada pembahasan a.)
⇔ m∠CBD =3.(10)⁰
⇔ m∠CBD =30⁰
jadi, besar sudut CBD adalah 30⁰


Contoh soal 3
Perhatikan gambar berikut!

Tentukan
Jika m∠DEG = (3x-6)⁰ dan  m∠FEG =(2x-4)⁰
a. besar sudut DEG
b. besar penyiku sudut DEG


a. menentukan nilai x terlebih dahulu
m∠DEG + m∠FEG =90⁰ (karena saling berpenyiku)
⇔  (3x-6)⁰ +  (2x-4)⁰=90⁰
⇔  (3x+2x-6-4)⁰ = 90⁰
⇔  (5x-10)⁰ = 90⁰
⇔  5x = 90 + 10
⇔  5x = 100
⇔  x = 100 : 5
⇔  x = 20
jadi, nilai x adalah 20

dilanjutkan menentukan m∠DEG
m∠DEG =(3x-6)⁰  (nilai  x = 20 sudah di temukan pada pembahasan a.)
⇔ m∠DEG = (3.(20)-6)⁰
⇔ m∠DEG = (60-6)⁰
⇔ m∠DEG = 54⁰
jadi, besar sudut DEG adalah 54⁰

b. menentukan besar penyiku sudut DEG
penyiku ∠DEG = ∠FEG   (ingat ya ∠FEG  adalah penyiku dari ∠DEG)
maka, 
m∠FEG= 90⁰ - m∠DEG 
⇔ m∠FEG= 90⁰ - 54⁰
⇔ m∠FEG= 36⁰
jadi, besar pelurus sudut DEG adalah 36⁰


C. SUDUT SALING BERTOLAK BELAKANG
Perhatikan gambar sudut berikut!

Pasangan ∠AOC dan ∠BOC membentuk ∠AOB sehingga saling berpelurus.
Begitu pula, pasangan ∠AOD dan ∠BOD membentuk ∠AOB sehingga saling berpelurus.
Selain itu,
Pasangan ∠AOC dan ∠BOD membentuk ∠COD sehingga saling berpelurus.
dan
pasangan ∠BOC dan ∠BOD membentuk ∠COD sehingga saling berpelurus.

Sedangkan,
pasangan ∠AOC dan ∠BOD  merupakan pasangan sudut saling bertolak belakang.
dan juga,
pasangan ∠AOD dan ∠BOC  merupakan pasangan sudut saling bertolak belakang.

Perhatikan pasangan ∠AOC dan ∠BOC dan  pasangan ∠BOC dan ∠BOD 
karena sudut-sudut tersebut saling berpelurus maka berlaku,
m∠AOC + m∠BOC=  180⁰, maka m∠AOC =  180⁰ -  m∠BOC       (1)
m∠BOC + m∠BOD=  180⁰, maka m∠BOD=  180⁰ -  m∠BOC        (2)
Dari (1) dan (2) diperoleh m∠AOC = m∠BOD =  180⁰ -  m∠BOC 
artinya besar sudut AOC sama besar dengan besar sudut BOD

Dengan cara yang sama, dapat diperoleh bahwa m∠BOC = m∠AOD artinya besar sudut BOC sama besar dengan besar sudut AOD

Kesimpulan
Sudut-sudut yang saling bertolak belakang memiliki besar sudut yang sama.

Contoh Soal 1

 Tentukan nilai a, b, dan c!





Pembahasan
i) a⁰ = 40⁰                 (saling bertolak belakang)
ii) b⁰ + 40⁰ = 180⁰    (saling berpelurus)
     ⇔ b⁰  = 180⁰  -  40⁰
     ⇔ b⁰  = 140⁰
iii) c⁰ = b⁰               (saling bertolak belakang)
     ⇔ c⁰  = 140⁰

Contoh soal 2

Tentukan nilai x, y, dan z!









Pembahasan
i) menentukan nilai x
    m∠FLH = m∠KLM   (saling bertolak belakang)
  ⇔ 7x⁰ = 49⁰
  ⇔ x = 49 : 7
  ⇔ x = 7

ii) menentukan nilai y
    m∠KML= m∠GMI   (saling bertolak belakang)
   ⇔ 4y⁰ = 76⁰
   ⇔ y = 76 : 4
   ⇔ y = 19

iii)menentukan nilai z
    m∠JKL= m∠EKM   (saling bertolak belakang)
   ⇔ (2z+35)⁰ = 125⁰
   ⇔ 2z = 125-35
   ⇔ 2z = 90
   ⇔ z = 45


Demikian materi hubungan antar sudut bagian pertama, semoga materi ini bermanfaat.

Jika menurut kalian materi ini bermanfaat, silahkan dapat di share dan di komen.
Penyusun juga menerima koreksi, kritik, dan saran yang membangun agar blog ini dapat lebih bermanfaat bagi semua orang.